A.I. Mathematician? A Simplified Look at DeepMind’s AlphaTensor

Google DeepMind’s AlphaTensor is the beginning of AI-driven mathematical innovation.

Image Source

Google’s DeepMind research group recently developed “AlphaTensor.” the first AI system for discovering novel algorithms to perform fundamental tasks such as matrix multiplication. This application has brought innovations to the 50-year-old mathematical challenge of finding the fastest ways to multiply two matrices. Let’s decompose the significance of this discovery.

What is Matrix Multiplication?

Most of us first encountered matrix multiplication in middle or high school. It consists of a series of multiplication and additions in a pre-defined order used to find the product of two nth-degree tensors. The most famously taught mechanism for multiplying two matrices is using the dot product (Figure 1) of rows and columns.

Figure 1. matrix dot product — (Image by Author)

Outside of K-12 education, this mathematical operation influences modern computing and is a cornerstone of digital systems. Almost any data type that can be tokenized or encoded into a multi-dimensional representation of numbers will require some matrix multiplication. Image processing and computer vision applications benefit tremendously from efficient matrix operations.

Figure 2. Convolutional Neural Network Operations — Source

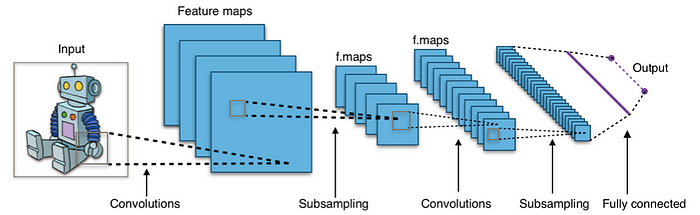
In a convolutional neural network (Figure 2), discrete convolutions are equivalent to taking a dot product between the filter weights and the values underneath the filter — in short, another matrix multiplication application.

For hundreds of years, mathematicians believed that the standard dot product was the best and most efficient method for multiplying matrices. That was until Colker Strassen introduced Strassen’s Algorithm (Figure 3) and shocked the world by demonstrating that more efficient algorithms exist. Strassen’s Algorithm utilized one less scalar multiplication than the traditional method.

Figure 3. Standard algorithm compared to Strassen’s algorithm, which uses one less scalar multiplication (7 instead of 8) for multiplying 2x2 matrices. Multiplications matter much more than additions for overall efficiency. (Image by Author)

Although Strassen’s Algorithm contains fewer arithmetic operations, it’s essential to consider that for current-generation CPUs, a multiplier can produce a result every machine cycle, but so can an adder. The multiplier takes more gates and has a longer latency to get the first result, but they are the same speed in throughput. Multiplication has a higher “big O” complexity than addition (Figure 4). In conclusion, Strassen was more efficient because he performed one less multiplication step.

Figure 4. The computational complexity of mathematical operations — source

AlphaTensor takes this further by using AI techniques to discover new matrix multiplication algorithms by optimizing through self-play and reinforcement learning.

What is Deep Reinforcement Learning?

Deep Reinforcement Learning (Deep RL) leverages the power of deep neural networks to optimize the solution to a particular problem. We adopt the concepts of agents, environments, and rewards as models of real-world systems where the goal is for an agent to maximize its reward in a particular environment.

Figure 5. Chess Board — Image Source

Suppose you consider the game of chess (Figure 5), where the objective is to capture your opponent’s pieces and checkmate their king. In that case, there exist a set of optimum moves for every possible scenario on the board that will maximize the odds of success. For this scenario, the RL schema could be defined as follows:

• The agent would be the chess player.
• The environment would be the board and all the pieces.
• The reward framework:
  — add 2pts for moving close to the opponent’s side of the board
  — add 5pts for capturing a pawn
  — add 10pts for capturing a knight or bishop
  — add 50pts for capturing the queen
  — subtract 10pts for losing any piece
  — subtract 50pts for losing your queen

We would award the appropriate reward for each move until either player is in check-mate or there is a draw (Figure 6). This process would be performed iteratively until our model scores are consistently high enough to meet our needs.

Figure 6. Reinforcement Learning Training Cycle — Individual Images from Microsoft Powerpoint 2022 (Image by Author)

AlphaTensor does something very similar to uncover the most optimum combinations of mathematical operations to perform matrix multiplication in a novel and efficient manner.

How is AlphaTensor Automating Algorithmic Discovery?

Using the concept of self-play, the team at DeepMind built their reinforcement learning schema for optimizing the matrix multiplication problem.

Image Source

Their schema, as described in their paper, looks something like this:

• The AlphaTensor agent starts without knowledge of existing matrix multiplication algorithms and is responsible for compiling a set of operations to minimize the error between the correct value of the matrix multiplication and its result.
• The environment is the actual definition of the matrices being operated on. In this case, DeepMind uses a 3D tensor.
• The reward is defined as a combination of the measure of the error in the result of the new algorithm and the number of steps taken to zero out the tensor (address all components of the matrices involved).

This schema results in a search space where the possible algorithms vastly outnumber the atoms in the universe. For reference, the possible moves at each step in the game of Go (Figure 7), which DeepMind solved years ago, is 30 orders of magnitude less than the complexity encountered by AlphaTensor.

Figure 7. Go Boardgame — Image Source

To increase the feasibility of this effort, AlphaTensor employs “a novel neural network architecture that incorporates problem-specific inductive biases, a procedure to generate useful synthetic data, and a recipe to leverage symmetries of the problem.”

Over time, the DeepMind team observed improvements in AlphaTensor’s ability to rediscover feasible algorithms such as Strassen’s and eventually surpass the human-defined methods in favor of algorithms faster than anything explored.

In a test where 5x5 and 5x5 (Figure 8) matrices were multiplied using Strassen’s Algorithm and AlphaTensor, we find that AlphaTensor can solve the operation in 76 multiplications versus Strassen’s 80!

Figure 8. Example of a 5x5 Matrix Multiplication (Image by Author)

Why is this a big deal?

AlphaTensor has helped shed light on the richness of matrix multiplication algorithms. These learnings will undoubtedly shape the future of the speed and efficiency of multi-dimensional data processing.

AlphaTensor has also proven that machine learning techniques can be used to discover mathematical innovation that surpasses human ingenuity. This flavor of deep reinforcement learning is in its early days, and the AlphaTensor work serves more as proof of feasibility than an immediate solution. This is an exciting step forward in computational optimization and self-optimizing AGI.

DeepMind’s GitHub includes a few of the algorithms that AlphaTensor has discovered and a jupyter notebook with instructions for loading and testing them. I’ve linked it below in the sources.

Don’t forget to follow my profile for more articles like this!

Sources:

• Discovering novel algorithms with AlphaTensor | https://www.deepmind.com/blog/discovering-novel-algorithms-with-alphatensor
• Computational complexity of mathematical operations | https://en.wikipedia.org/wiki/Computational_complexity_of_mathematical_operations#Arithmetic_functions
• AlphaTensor GitHub | https://github.com/deepmind/alphatensor
• Discovering faster matrix multiplication algorithms with reinforcement learning | Fawzi, A. et al. | https://www.nature.com/articles/s41586-022-05172-4